
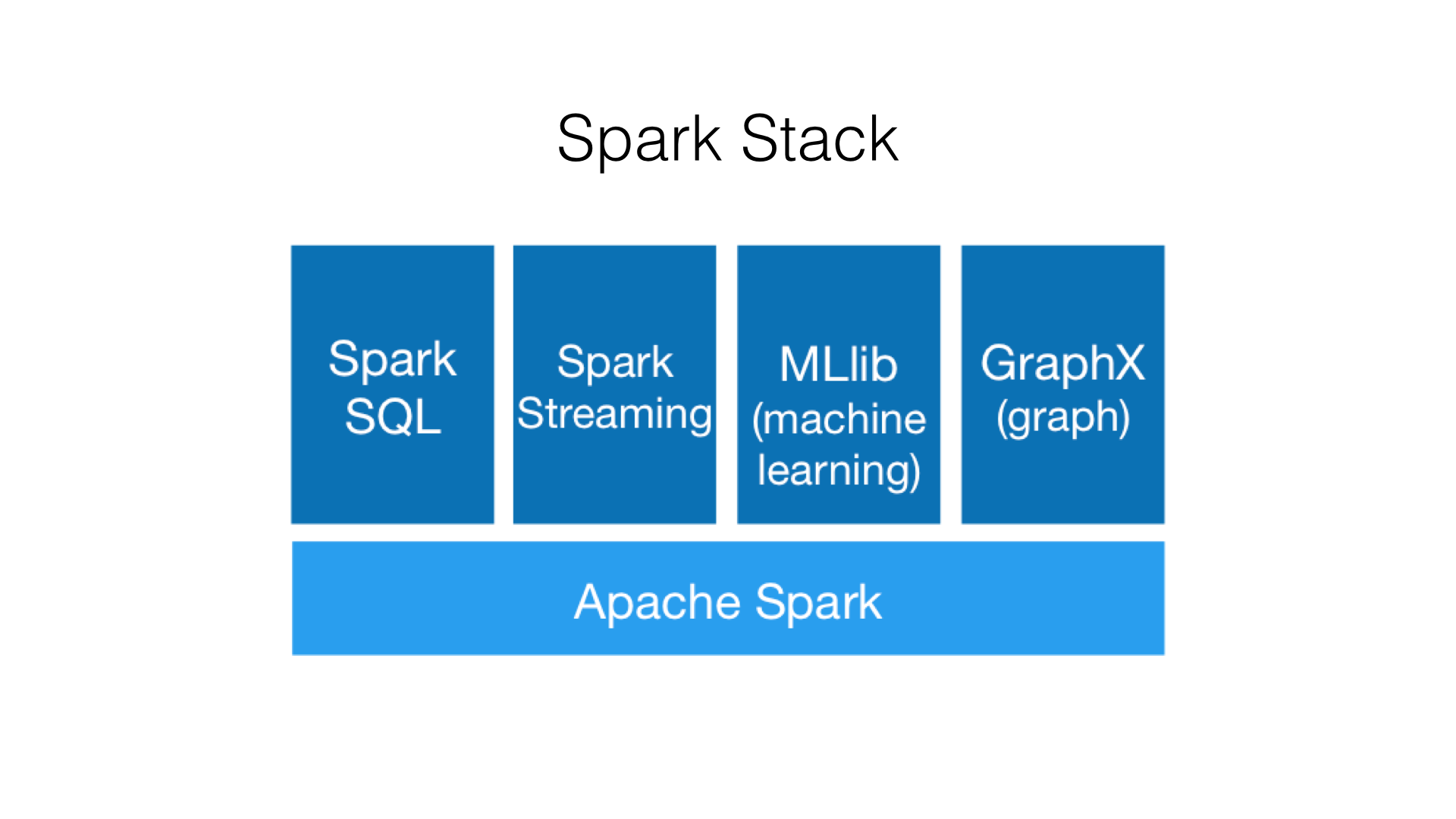
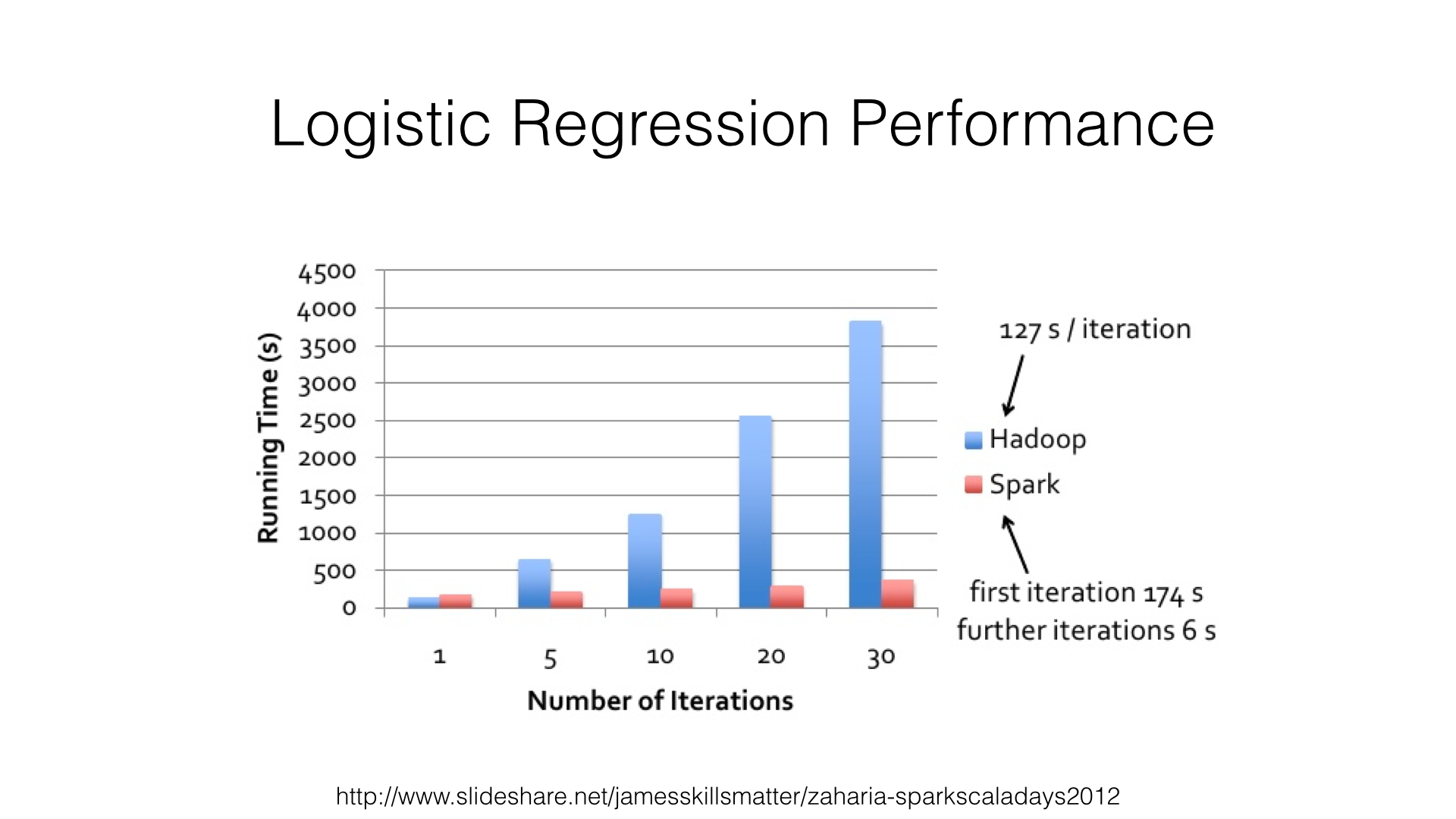
Resilient Distributed Datasets (RDDs)¶
Basic abstraction in Spark. Fault-tolerant collection of elements that can be operated on in parallel
RDDs can be created from local file system, HDFS, Cassandra, HBase, Amazon S3, SequenceFiles, and any other Hadoop InputFormat.
Different levels of caching: MEMORY_ONLY, MEMORY_AND_DISK, DISK_ONLY, OFF_HEAP, etc
Rich APIs for Transformations and Actions
Data Locality: PROCESS_LOCAL -> NODE_LOCAL -> RACK_LOCAL
In [1]:
from pyspark import SparkContext, SparkConf
from pyspark.sql import SQLContext, HiveContext
import py4j
conf = SparkConf().setAppName("IntroSparkJupyter") \
.setMaster("local[2]")
# conf = SparkConf().setAppName("IntroSparkJupyter") \
# .setMaster("yarn-client") \
# .set("spark.executor.memory", "512m") \
# .set("spark.executor.cores", 1) \
# .set("spark.executor.instances", 2)
sc = SparkContext(conf=conf)
try:
# Try to access HiveConf, it will raise exception if Hive is not added
sc._jvm.org.apache.hadoop.hive.conf.HiveConf()
sqlContext = HiveContext(sc)
except py4j.protocol.Py4JError:
sqlContext = SQLContext(sc)
except TypeError:
sqlContext = SQLContext(sc)
sc
Out[1]:
In [2]:
rdd = sc.parallelize(xrange(10, 0, -1)).cache()
In [3]:
rdd.count()
Out[3]:
In [4]:
rdd.collect()
Out[4]:
In [5]:
rdd.sample(False, 0.2).collect()
Out[5]:
In [6]:
rdd.sortBy(lambda x: x, ascending=True).collect()
Out[6]:
In [7]:
rdd.filter(lambda x: x>5).collect()
Out[7]:
In [8]:
rdd.map(lambda x: x*2).collect()
Out[8]:
In [9]:
from operator import add
rdd.reduce(add)
Out[9]:
In [25]:
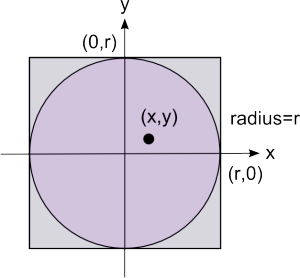
# Calculating Pi with the Monte Carlo method
# https://learntofish.wordpress.com/2010/10/13/calculating-pi-with-the-monte-carlo-method/
import random
import math
def withinCircle(x,y):
if(x**2+y**2<1):
return True
else:
return False
def main():
circleArea = 0
squareArea = 0
pi = 0
for i in range(0,1000000):
x = random.random()
y = random.random()
if(withinCircle(x,y)==1):
circleArea=circleArea+1
squareArea=squareArea+1
pi = 4.0*circleArea/squareArea
print "Approximate value for pi: ", pi
print "Difference to exact value of pi: ", pi-math.pi
print "Error: (approx-exact)/exact=", (pi-math.pi)/math.pi*100, "%"
main()
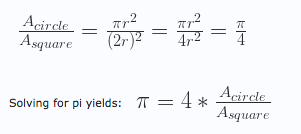
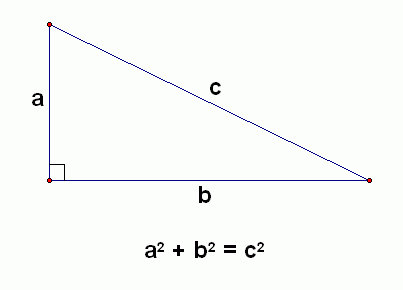
In [27]:
from random import random
import math
def f(_):
x = random()
y = random()
if x ** 2 + y ** 2 < 1:
return 1
else:
return 0
n = 1000000
count = sc.parallelize(xrange(1, n)).map(f).reduce(add)
print("Pi is roughly {}".format( 4.0 * count / n))
In [11]:
sc.stop()